WS23 971007 VU Advanced Methods and its Applications - Performance topics

Not the most efficient way of computing π\pi

As we very well know, there are a lot of ways to compute π\pi. There is even a blog entry in the Julia blog for that. Nevertheless, we decided for a different method (that is part of the introductory courses on JuliaAcademy).

A circle with radius rr has an area of

Acircle=πr2A_{circle} = \pi r^2
and the square that encases it
Asquare=4r2.A_{square} = 4 r^2.

The ratio between the area of the circle and the area of the square is

AcircleAsquare=πr24r2=π4 \frac{A_{circle}}{A_{square}} = \frac{\pi r^2}{4 r^2} = \frac{\pi}{4}
and therefore we can define π\pi as
π=4AcircleAsquare. \pi = 4\frac{A_{circle}}{A_{square}}.
The same is true if we just take the first quadrant, so 14\frac14 of the square as well as the circle. This simplification will make the code more compact and faster.

The above formula suggests that we can compute π\pi by a Monte Carlo Method. Actually this example is also included in the Wiki article and it comes with this nice gif.

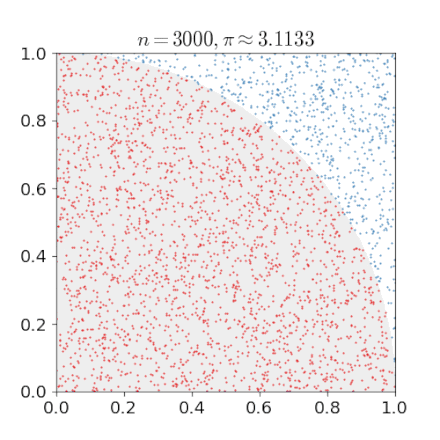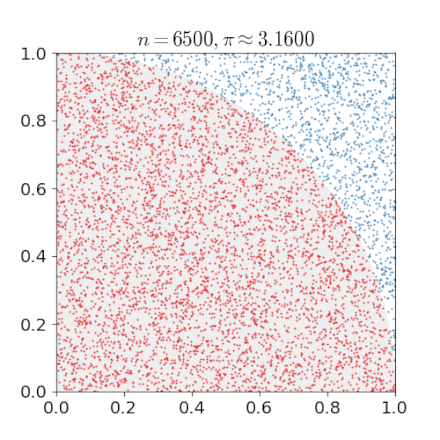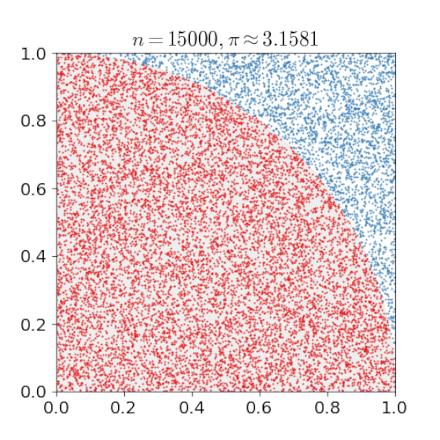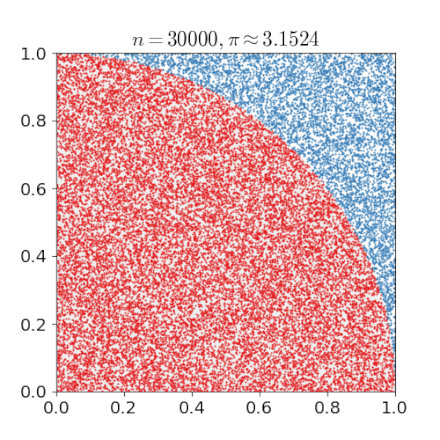
Simulation of the Monte Carlo Method for computing π.
Simulation of the Monte Carlo Method for computing π. Original source:

https://commons.wikimedia.org/wiki/File:Pi_30K.gif

The algorithm therefore becomes:

  1. For a given number NN of uniformly scattered points in the quadrant determine if these points are in the circle (distance less than 1) or not. We call the number of points in the circle MM.

  2. Estimate π\pi by computing

π≈4MN. \pi \approx 4 \frac{M}{N}.

For the following Exercises, we will use and complete the following code stub:

# You will need some Packages. Add them here by using <PACKAGE>.

function sample_M_non_distributed_rng(N::Int64, rng::AbstractRNG)
    # Exercise 1 (pt 1/2)
    return nothing
    # Exercise 1 end
end


function estimate_pi(N::Int64, method::Symbol)
    function sample_M_non_distributed(N::Int64)
        return sample_M_non_distributed_rng(N, Random.default_rng())
    end

    function sample_M_threaded(N::Int64)
        # Exercise 2
        return nothing
        # Exercise 2 end
    end

    function sample_M_threaded_atomic(N::Int64)
        # Exercise 3
        return nothing
        # Exercise 3 end
    end

    function sample_M_threaded_tasksafe(N::Int64)
        # Exercise 4
        return nothing
        # Exercise 4 end
    end

    function sample_M_threaded_over_buckets(N::Int64)
        # Exercise 5
        return nothing
        # Exercise 5 end
    end

    function sample_M_threaded_over_buckets_rng(N::Int64)
        # Exercise 6
        return nothing
        # Exercise 6 end
    end

     function_mapping = Dict(
         :ex1 => sample_M_non_distributed,
         :ex2 => sample_M_threaded,
         :ex3 => sample_M_threaded_atomic,
         :ex4 => sample_M_threaded_tasksafe,
         :ex5 => sample_M_threaded_over_buckets,
         :ex6 => sample_M_threaded_over_buckets_rng,
     )

     M = function_mapping[method](N)

    # Exercise 1 (pt 2/2)
    return nothing
    # Exercise 1 end
end
Implement the above described algorithm to compute π\pi.

  1. Complete the function sample_M_non_distributed which samples MM for given N and random number generator rng.

  2. At the bottom of estimate_pi use MM to compute an estimate for π\pi. Also compute the absolute error and return both values.

  3. Test your code with different values for NN. You can run your implementation like this: estimate_pi(N, :ex1) (define N beforehand).

  4. Benchmark your naive implementation (we will keep improving it later).

Hint: The function rand() (without additional arguments) generates a random sample from a uniform distribution spanning the interval [0,1][0,1]. You can also pass rng to rand() for using a specific random number generator.

Solution 

using BenchmarkTools
using Random


function sample_M_non_distributed_rng(N::Int64, rng::AbstractRNG)
    M = zero(Int64)

    for _ in 1:N
        if (rand(rng)^2 + rand(rng)^2) < 1
            M += 1
        end
    end

    return M
end


function estimate_pi(N::Int64, method::Symbol)
    function sample_M_non_distributed(N::Int64)
        return sample_M_non_distributed_rng(N, Random.default_rng())
    end

     function_mapping = Dict(
         :ex1 => sample_M_non_distributed,
     )

     M = function_mapping[method](N)

     est_pi = 4 * M / N

    return est_pi, abs(pi - est_pi)
end

N = 2^30

@btime estimate_pi(N, :ex1)

  3.718 s (4 allocations: 384 bytes)
(3.1414526104927063, 0.00014004309708681717)
CC BY-NC-SA 4.0 - Gregor Ehrensperger, Peter Kandolf. Last modified: January 18, 2024. Website built with Franklin.jl and the Julia programming language.